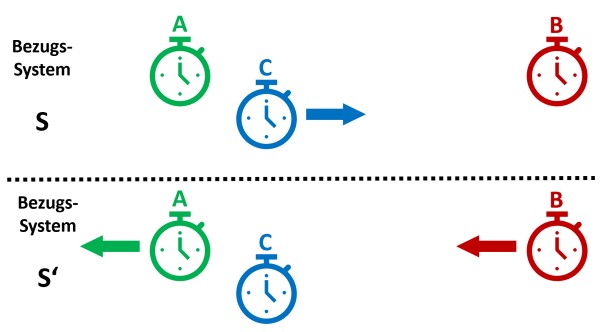
 Zuerst müssen wir uns die Bezugssysteme anschauen. Diese sind am Uhrenbeispiel in der Graphik links skizziert. Im ersten Bezugssystem S bewegt sich die Uhr C relativ zu den hier ruhenden Uhren A und B. Der Beobachter ruht ebenfalls. Im zweiten Bezugssystem S‘ bewegen sich die Uhren A und B relativ zu C (in die genau andere Richtung). Hier sitzt der Beobachter sozusagen auf der Uhr C. Nach der Relativitätstheorie sieht jeder Beobachter die jeweils relativ zu ihm bewegte Uhr langsamer gehen.
Zuerst müssen wir uns die Bezugssysteme anschauen. Diese sind am Uhrenbeispiel in der Graphik links skizziert. Im ersten Bezugssystem S bewegt sich die Uhr C relativ zu den hier ruhenden Uhren A und B. Der Beobachter ruht ebenfalls. Im zweiten Bezugssystem S‘ bewegen sich die Uhren A und B relativ zu C (in die genau andere Richtung). Hier sitzt der Beobachter sozusagen auf der Uhr C. Nach der Relativitätstheorie sieht jeder Beobachter die jeweils relativ zu ihm bewegte Uhr langsamer gehen.
Das Paradoxon kann gelöst werden, wenn man daran denkt, dass die verschiedenen Uhren vor der Startzeit der Messung (oder Beobachtung) synchronisiert werden müssen. Synchronisiert man als Beobachter im Bezugssystem S die Uhren A und B mit Lichtsignalen, kann man die hier bewegte Uhr C zum Startzeitpunkt ebenso synchronisieren. Man beobachtet dann, dass die Uhr C langsamer geht, als die Uhren A und B (die Zeit wird proportional zum Lorentzfaktor gedehnt).
In S‘ jedoch synchronisiert man die Uhren A und B von der Uhr C aus. B bewegt sich jedoch auf C zu, während A sich entfernt. Die Lichtgeschwindigkeit ist in beiden Bezugssystem gleich groß, das Licht hat aber unterschiedlich lange Wege zurückgelegt, um an den jeweiligen Uhren anzukommen. Somit laufen im Bezugssystem S‘ die Uhren A und B bereits zum Start der Messung unterschiedlich. Die Uhr A fängt später an zu laufen, während B einen Frühstart hinlegt. Da sich in S‘ die Uhren A und B bewegen, gehen diese nach der Relativitätstheorie langsamer, als Die Uhr C.
Vergleicht man nun die Zeitdauer, die die Uhr C in S braucht, um sich von A nach B zu bewegen mit der Zeitdauer, die die Uhren A und B in S‘ brauchen, um sich an C vorbeizubewegen, muss man die unterschiedlich laufenden Uhren in S‘ berücksichtigen und mit der tatsächlich gemessenen Zeitdauer verrechnen. Man misst somit letztendlich die „Eigenzeiten“ (grob gesagt die Zeitdauer) der Uhren A und C (oder B und C). Die Eigenzeit ist in beiden Bezugssystemen invariant, also identisch, obwohl es so aussieht, als würden die jeweils bewegten Uhren während der Messung unterschiedlich schnell gehen.